前回は「45°が一番遠くに飛ぶ」と言われる理由を解説しました。
前回の投稿はこちら!
今回は、なぜ実際には45°ではないのか 解説していきます!
結論
- 地面から発射されるわけではなく、高さが関係しているため
- 最大距離や最適な角度には初速度と高さが変数としてあるため
実際は45°ではないのか、検証(下記にコードあり)
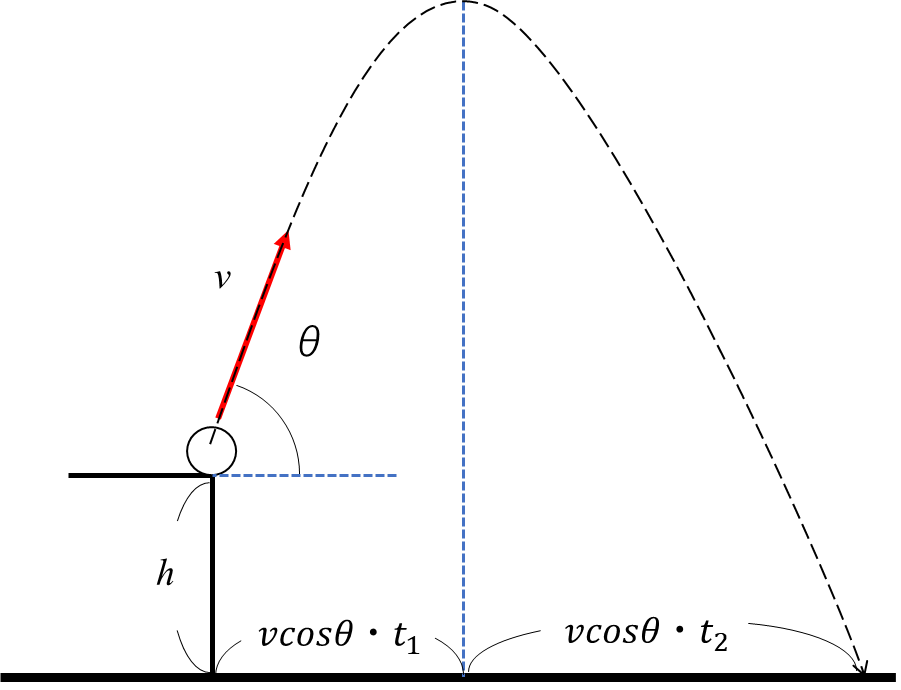
投げ始めてボールが最も高い高さに届くまでの時間を $t_1$ とし 、
最も高い高さから地面に落ちるまでの時間を $t_2$ とします。
垂直方向について考える
$t_1$ について解くのは前回の基礎的な斜方投射と同じです。
$$t_{1}=\frac{v\sin\theta}{g}\tag{1}$$
次は$t_2$について考えます。
左辺を「高さ$h$ の場所から垂直方向に速度$v\sin\theta$で投げた時の$t_1$ 秒後の高さ」とし、
右辺を「最も高い高さから地面に落ちるまでの$t_2$秒間の自由落下する距離」とします。
$$h+v\sin\theta t_{1} – \frac{1}{2}gt_{1}^{2}=\frac{1}{2}gt_{2}^{2}\tag{2}$$
①の式を②を代入し、$t_2$について解きます。
$$h+\frac{(v\sin\theta)^{2}}{g}-\frac{(v\sin\theta)^{2}}{2g}=\frac{1}{2}gt_{2}^{2}$$
$$h+\frac{(v\sin\theta)^{2}}{2g}=\frac{1}{2}gt_{2}^{2}$$
$$t_{2}^{2}=\frac{2h}{g}+\frac{(v\sin\theta)^{2}}{g^{2}}$$
$t_2 > 0$なので
$$t_2=\sqrt{\frac{2h}{g}+\frac{(v\sin\theta)^{2}}{g^{2}}}\tag{3}$$
水平方向について考える
距離は 速度×時間 なので、式自体は以下のようになります。
$$d=v\cos\theta・(t_{1}+t_{2})\tag{4}$$
(4)に$t_1,t_2$について解いた式(1)(3)を代入します。
$$d=v\cos\theta・(\frac{v\sin\theta}{g}+\sqrt{\frac{2h}{g}+\frac{(v\sin\theta)^{2}}{g^{2}}})$$
$$d=\frac{v\cos\theta}{g}・(v\sin\theta+\sqrt{2gh+(v\sin\theta)^{2}})$$
この式を$\sin\theta$を取り出してもう少し見やすく、倍角の公式を使うと、以下のようにします。
$$d=\frac{v^{2}\sin2\theta}{2g}・(1+\sqrt{\frac{2gh}{(v\sin\theta)^{2}}+1})\tag{5}$$
しかし、上記の式に$\theta=45$を入れても最大値にはなりません。
人間の手では膨大な時間がかかってしまいますので、ここはプログラミングで
解を求めていきます。
コード
Pythonで書いてみました。内容は、balloptimize()という関数を定義し、
その引数に初速度と高さを入れれば最適な角度とその時の距離を出力する処理となっています。
出力時は小数点以下が膨大になるので四捨五入してスッキリ見せています。
import math
import numpy as np
def balloptimize(v,h):
g = 9.8 #重力加速度
h = h/100 #cmをmに換算
deg = np.arange(1, 90, 0.01) #1~90までの0.01刻みの配列を生成
deg_list = list(deg) #np.array型をlist型にする
dest_list = [] #結果を入れるリストを用意
for i in range(len(deg_list)):
dest = ((v ** 2 * math.sin(math.radians(2 * deg_list[i]))) / (2 * g)) * (1 + (( 2 * g * h ) / ((v * math.sin(math.radians(deg_list[i])))) ** 2 + 1)**(1/2)) #式⑤
dest_list.append(dest)
print("-----最大飛距離[m]-----")
print(round(max(dest_list),2))
print() #改行
print("-----最適な角度[deg]-----")
print(round(deg_list[dest_list.index(max(dest_list))],2))
では、初速度$20[m/s]$ , 高さ$100[cm]$を第一引数、第二引数に代入してみます。
<実行結果>
balloptimize(20,100)
-----最大飛距離[m]-----
41.8
-----最適な角度[deg]-----
44.31
まとめ
- 「45°が最も遠くに飛ぶ」のは、高さが0のときだけ!
- 投げる時に高さがある場合、最も遠く飛ぶ角度は 45°未満になる




コメント