みなさんは小さい頃、学校で体力測定でボール投げをやったことはありますか?
私の学校でも握力やらシャトルランやら様々な種目があり、
その中でも私はボール投げがニガテでした。
当時の担任のA先生は「ボール投げは算数ができれば遠くまで投げれるぞ!」
と仰っていましたが、小さい頃の私は理解ができませんでした。。
さて、今回は「45°が遠くまで飛ぶ」という通説の理由とその証明、
そして次回は「最も遠くに飛ばせる要因」について解説していきます!
また、前提知識として 高校の 数学 と 物理 の知識が必要になります!
「45°が最も遠くまで飛ぶ」と言われているワケ
こちらは高校物理の斜方投射の復習となります。
では、基礎を振り返ってみましょう!
物体の初速度を v 、その時の投げる角度を θ とします。
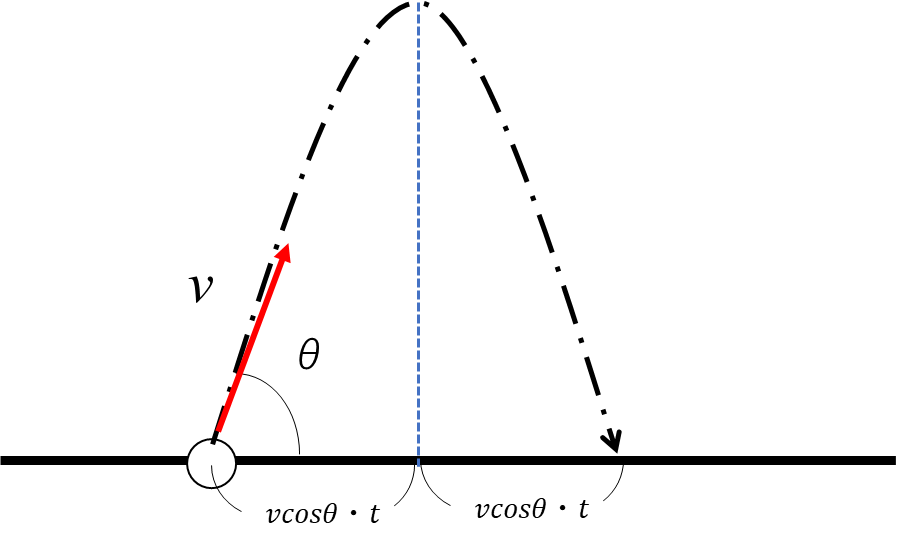
垂直方向について考える
投げ始めてボールが最も高い高さに届くまでの時間を t[s] とします。
最も高い高さでは、垂直方向の速度が 0 [m/s] になりますので、
$$ 0 = v \sin\theta – gt $$
となり、これを t について解きます。
$$ t = \frac{v\sin\theta}{g} \tag{1}$$
ボールが最も高い高さに届くまでの時間を t としましたので、
投げ始めて落ちるまでにかかる時間は 2t になります。
水平方向について考える
距離の式は、時間×速度 で表せますので、
距離 d = 水平方向の速度×投げ始めて落ちるまでの時間 になります。
まず、これを式に表してみましょう。
$$ d=v\cos\theta × 2t \tag{2}$$
式を代入し、最大となる角度を調べる
(1)を(2)に代入します。
$$ d=v\cos\theta × \frac{2v\sin\theta}{g}$$
$$ d=\frac{2v^{2}\sin\theta\cos\theta}{g} $$
ここで 高校数学の 倍角の公式 を使用します。
<倍角の公式>
$$ \sin2\theta=2\sin\theta\cos\theta $$
上記の倍角の式を代入しますと、以下のようにスッキリ見やすくなります。
$$ d=\frac{v^{2}\sin2\theta}{g}$$
さて、距離 d を最大をする場合、sin の値が 1 になればよいので、
$$\sin2\theta=1$$
$$2\theta=90$$
$$\theta=45$$
となり 45°の時が最も遠くに飛ぶ と言われている根拠となります。
しかし、これは投げる場所と落ちる場所の高さが等しい場合のみ成り立ちます。
では、冒頭に述べた通り次回は 45°で投げれば最も遠くに飛ぶわけではない理由 に解説します。
(今回初めて Latex で数式書いた….)



コメント